「どの組合せの制服が魅力的か? -心理学実験による統計分析-」の探究活動
皆さん、こんにちは。テラオカ電子です。今回は、2012年度のもので、少し古い活動なのですが、心理学と統計の分野に挑戦したものを紹介します。面白いと思いますので最後までお付き合いください。
この探究活動のメンバーは、第19回のブログ記事で紹介した女子生徒4名です。いつものように、彼女らがサイエンスコンテストで発表した内容を私が代読した形ですが、YouTubeで一般公開しました。以下のリンクから動画を視聴できます。見て頂けると後の話が良く分かると思います。
【テラオカ電子:「「どの組合せの制服が魅力的か」(2012)を公開します。」はこちらから】
どの組合せの制服が魅力的か ―心理学実験による統計分析―
【1 はじめに】
私たちパソコン同好会は、パソコンを活用した応用技術を学んでいます。今回、私たちは、心理学実験の統計分析に取り組みました。私たちの学校の制服は、色々な組合せで着ることができます。女子の場合、色や模様の違う、リボン、ブレザー、スカートがそれぞれ3、4種類用意されており、自分の好みに合わせて選べます。一方で、どの組合せが自分にとって一番魅力的なのかを判断することが悩ましい所です。そこで、制服の組合せの魅力度を数値化して表すことができなかと考えました。調査した結果、人の好みを数値化するには、心理学実験があることを知りました。また、得られたデータを実験計画法という統計分析で様々なことが分かることを知りました。
[心理学に関して私は専門外ですので、放送大学の所属している学習センターの心理学がご専門の先生に、生徒を引率してインタビューに行きました。これについては、また機会があれば述べます]
本研究では、まず、Adobe社の Photoshop CS6を使って、色々な組合せの制服の合成写真を作成しました。次に、それを被験者に点数を付けてもらい、Excelを使って、実験計画法により効果や分散分析を行い、最適な制服の組合せについて検討しました。
[実験計画法に関して、私はすごい専門家というわけではないのですが、エンジニア時代に取り組んだことがあります。自分の知識を証明したいわけではないのですが、「QC検定2級」を持っています]
【2 目的】
本研究では、まず、合成写真の顔は、国民的アイドルであるAKB48の前田敦子さんとします。従って、前田さんが高校に入学して制服を着た場合の似合い度を測定することになります。合成写真の背景の影響を考察するため背景なし、市街地の2パターンを準備します。また、アンケートの被験者の属性による違いも検討するため、男女の高校生、男女の先生に協力を頂きます。さらに、アンケートの方法に違いが出るかどうかも検討するため、印刷の合成写真を見せて回答してもらう個別形式と、プロジェクターで投影して回答してもらう集合形式で行います。
[言うまでもありませんが、当時、前田敦子さんがセンターでした]
実験計画法は、リボン、ブレザー、スカートの単独の影響をみる主効果だけでなく、リボンとブレザーなどとの繋がりの影響をみる交互作用も測定するため3水準系直交配列表のL27(313)を使います。それを使う分散分析により、一番ベストな組合せが求まり、組合せのバランスである交互作用も求まります。これらの結果から最適な制服の組合せについて検討します。
最後に、私たちは、モノづくりは、製品の機能や性能はもちろん大切ですが、それに加えて、デザインも重要であると考えています。今回の研究方法で、デザインを評価することができるかどうかも考察します。
【3 実験方法】
3-1 合成写真の作成と実験計画法
Adobe社の Photoshop CS6を使ってリボン、ブレザー、スカート、背景をレイヤーに配置して合成写真を作成しました。合成写真の例を図1、図2に示します。写真の制服の組合せは、表1の様に因子を配置して、表2の直交配列表L27(313)に従って割付けて27種類となります。
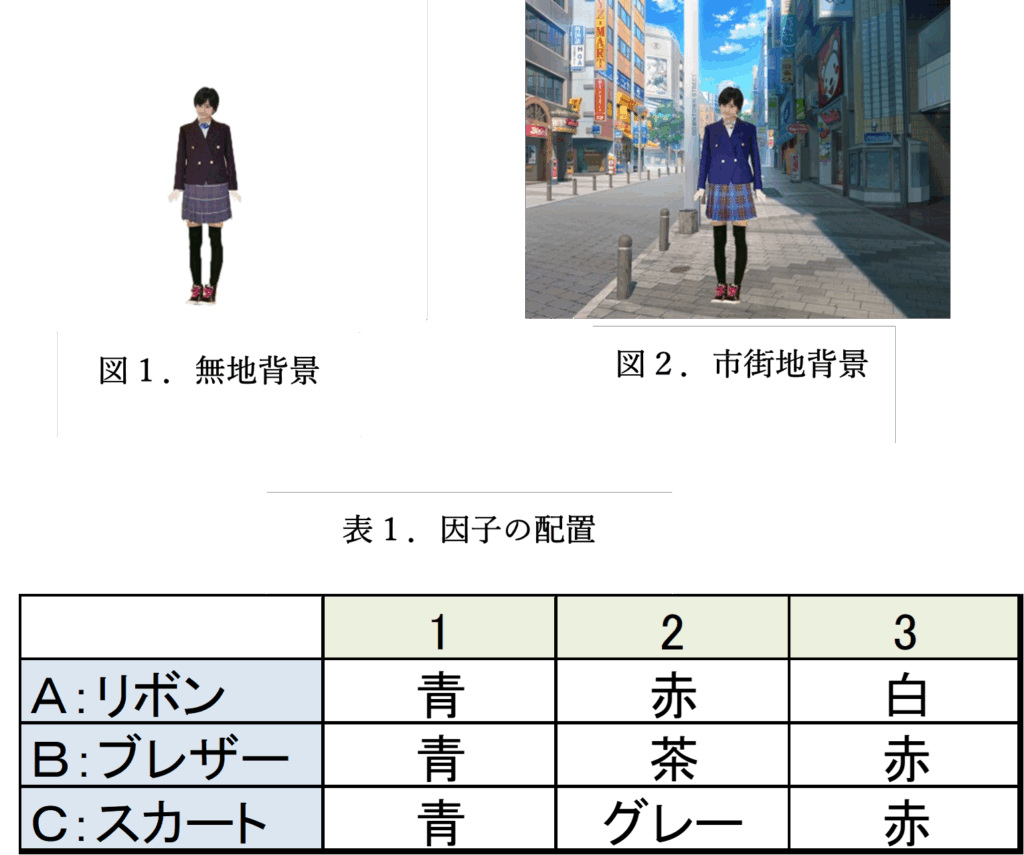
例えば、No17の写真は、A(リボン)は第3水準なので、A3(白色リボン)、同様にB2(茶色ブレザー)、C2(グレー色スカート)の写真となります。
Aリボンを第2列、Bブレザーを第1列、Cスカートを第5列に割付けると、3つの交互作用A*Bは第3列と第4列、B*Cは第6列と第7列、A*Cは第8列と第11列に現れます。

3-2 アンケートの実施
写真の被験者への提示はランダムな順にして、各写真を25点満点で採点してもらいました。印刷した写真を見せて採点してもらう個別形式と、プロジェクターで投影して採点してもらう集合形式で行いました。
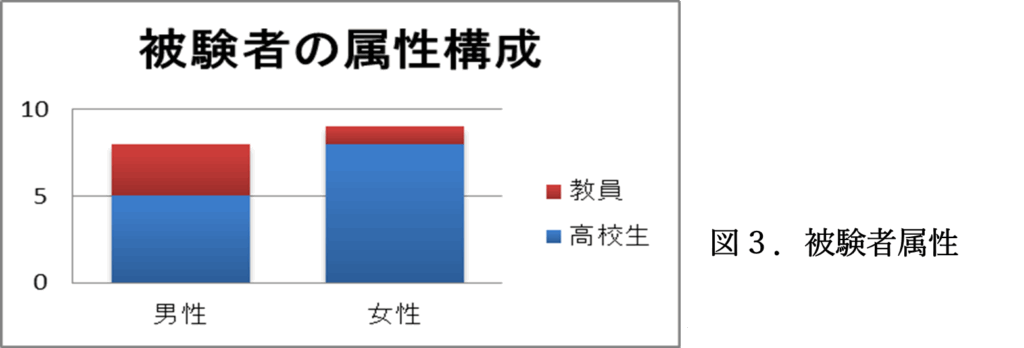
アンケートに回答して頂いた被験者の属性の内訳を、図3に示します。男性8名(教員3名含む)、女性9名(教員1名含む)にお願いしました。
[この学校は、このような活動を面白いと言ってくれる雰囲気がありました。生徒も楽しんで取り組めたのではないかと思います]
【4 実験結果】
4-1 採点結果
表2の一番右の列の数値は、デザインの専門の先生の採点結果です。写真は無地背景、アンケート方法は集合形式です。以降の分析では、この採点結果を分析していきます。これを取り上げたのは、この先生が、色彩の専門家であることと、本研究の意味をよく理解して頂き、採点を正確に回答してくれると考えたからです。
4-2 データ整理
データをグラフ化するにあたり、各列における水準ごとの合計と平均を求めます。結果を表3に示します。また、交互作用のために各組合せの平均を求めた二元表を表4に示します。

4-3 主効果グラフと交互作用グラフ
表3からA、B、Cの各因子について、各水準の平均をグラフにした、主効果のグラフを図4に示します。さらに、表4より各因子、各水準をグラフにした、交互作用のグラフを図5(AとBの交互作用)、図6(BとCの交互作用)、図7(AとCの交互作用)に示します。
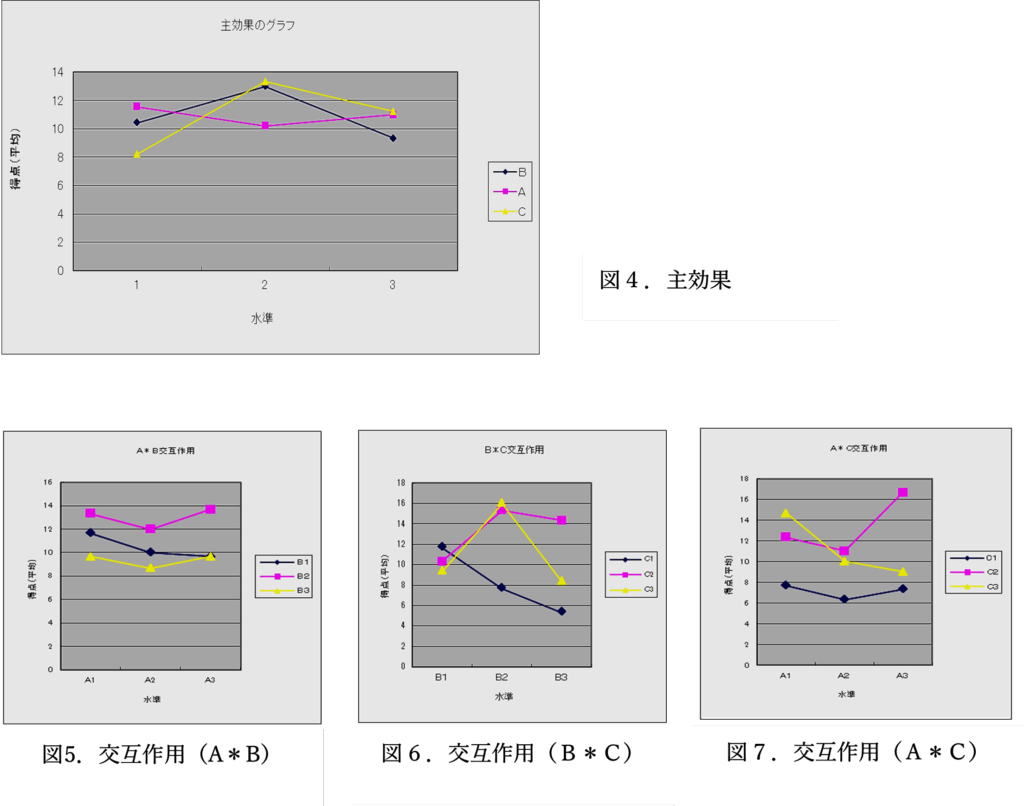
グラフより得点に変動がある、主効果B(ブレザー)、C(スカート)と、交互作用B*Cの効果があると予想されます。交互作用A*Cの効果はありそうにもみえますが、それほど大きくはなさそうです。交互作用A*Bの効果はなさそうです。
ブレザーとスカートの選び方で魅力度が変わりそうですが、リボンはそれほどでもないと思われます。また、ブレザーとスカートには、組合せ効果がありそうです。リボンとスカートの組合せは、はっきりしません。リボンとブレザーの組合せの効果は、なさそうです。
4−4 分散分析
13ある各の列の列平方和の結果を表5に示します。列平方和は以下の式で求めます。
S(列平方和)=(第1水準の合計)2/9+(第2水準の合計)2/9+(第3水準の合計)2/9

次に各要因について、要因の平方和を、その要因が割り付けられた列の列平方和として求め、交互作用の平方和は、割り付けられた2つの列平方和の合計として求めます。誤差の平方和は、何も割り付けられなかった列の平方和の合計です。
また、主効果の自由度は2で、交互作用の自由度は4です。誤差の自由度は誤差列の列自由度の和です。平均平方V(平方和S/自由度φ)、F0値(F分布)、P値(検定統計量が有意となる確率)を求めて分散分析表にまとめた結果を表6に示します。
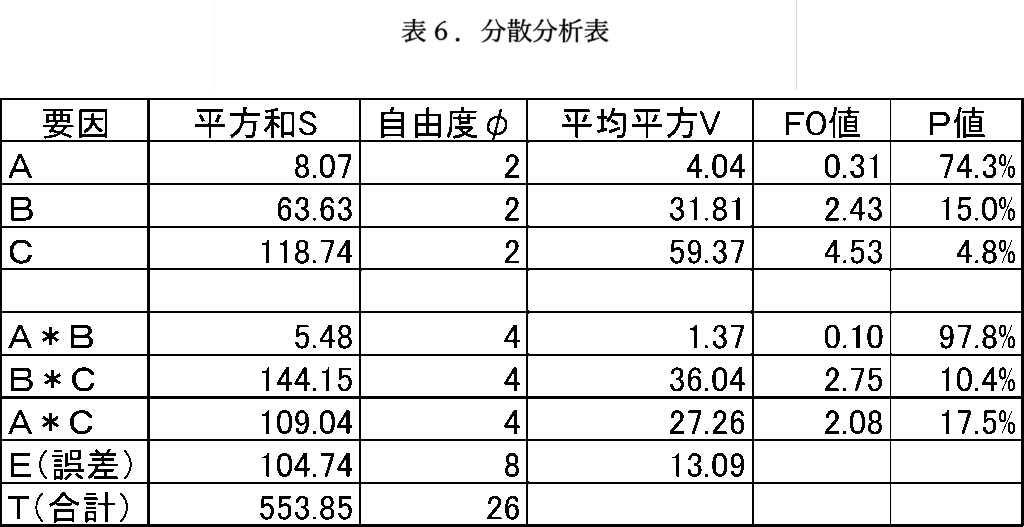
表6より主効果Cは、P値が5%以下なので有意となりました。交互作用B*Cは有意ではありませんが、F0値が小さくなくP値も約10%なので無視しません。
主効果Bは、交互作用B*Cがあるので残します。同様に、交互作用A*Cは、主効果Cがあるので残します。F0値が小さく、P値も大きい主効果Aと交互作用A*Bは誤差にプーリング(誤差に取り込む)します。
プーリング後の分散分析表の結果を表7に示します。

分散分析の結果、主効果Cが高度に有意(P値が1%以下)、主効果Bと交互作用B*CとA*Cが有意となりました。スカートがメインでブレザーがサブで効果があります。特にスカートは、ブレザーとリボンとの間で繋がりがあるので特に慎重に選ぶ必要がありそうです。
[このような計算ですが、実験計画法では、きちんと手順が決められています。なので、手法とその解釈をしっかり理解する必要があります]
4-5 最適水準における推定
因子Cは、図4よりC2水準、因子Bと因子Aは、表4の二元表よりB2、A3水準が選ばれます。すなわち、リボン(白)、ブレザー(茶)、スカート(グレイ)の組合せが最も魅力的な制服となりました。母平均の点推定値は、以下の式より求まります。
μ(A3,B2,C2)=(A3,B2水準の合計)/3+(C2水準の合計)/9-(総計)/27
=41.1/3+120/9-295/27
=16.1 ・・・(式2)
この結果、A3,B2,C2の制服での点数の母平均の点推定値は16.1点となりました。
27通りの制服のおけるNo.17の制服ですが、アンケート結果の17点とほぼ同じ値になりました。
4-5 被験者の差による違い
ある女子高校生の分散分析の結果(プーリング後)を表8に示します。これより、A(リボン)とC(スカート)の交互作用のみ有意となりました。主効果は有意になりませんでした。個々のアイテムを選ぶというよりは、リボンとスカートの組合せが大切という結果になりました。2元表より、A2(赤色リボン)、B3(赤ブレザー)、C3(赤色スカート)の組合せが高い得点となっています。これは、デザインの先生とは違う結果になりました。A*Cが有意であるところは一致しています。

男子の平均の分散分析の結果を表9に、女子の平均の分散分析の結果を表10に、全体の平均の分散分析の結果を表11に示します。
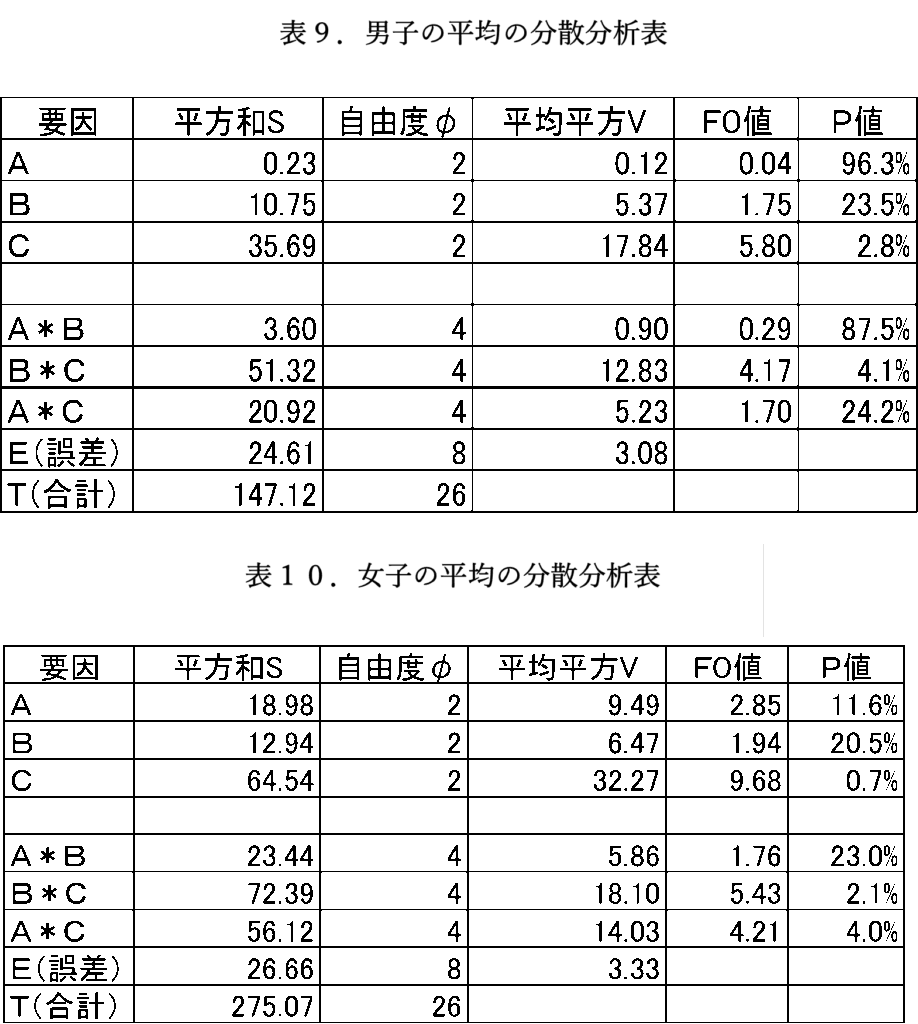
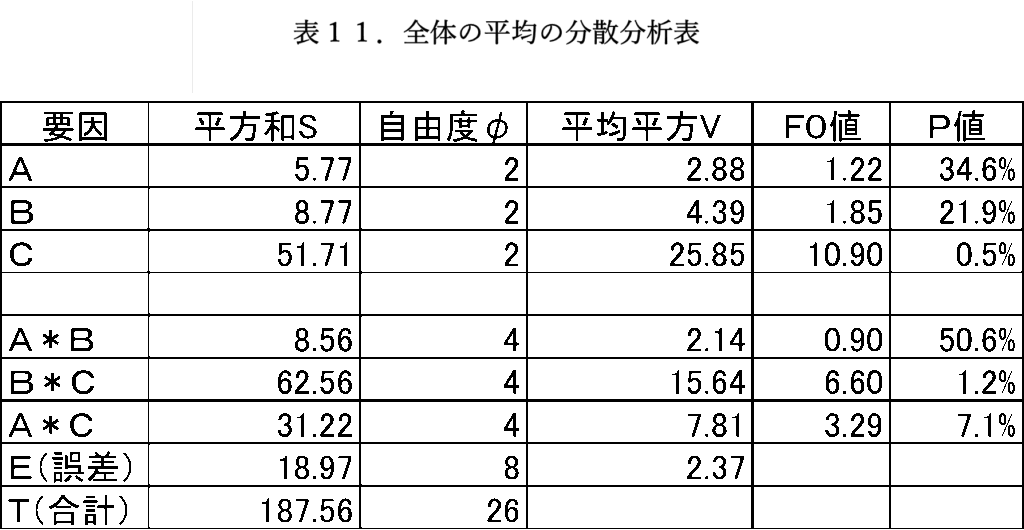
表9より男子は、因子Cと因子B*Cが有意となりました。女子はそれに加えてA*Cも有意となりました。全体では、因子Cが高度に有意となり、男子の結果を強めた結果になりました。スカートがメインで、スカートとブレザーの組合せが大切であるということになりました。最適水準は、いずれもA2(赤色リボン)、B3(赤色ブレザー)、C3(赤色スカート)となりました。
4-6 アンケート方法による違い
個別方式(サンプル数:7)での結果の平均値から求めた分散分析表を表12に、集合形式(サンプル数:15)での結果の平均値から求めた分散分析表を表13に示します。

表12より、個別方式では、因子Cと交互作用B*Cが高度に有意、交互作用A*Cが有意となりました。表13より集合形式では、因子Cが高度に有意、交互作用B*Cが有意となりました。交互作用A*Cは有意とはなりませんでした。このことより、個別形式の方が評価が鋭くなると考えられます。最適水準は、いずれもA2(赤色リボン)、B3(赤色ブレザー)、C3(赤色スカート)となりました。

次に、図1のような背景なしの写真による結果(サンプル数:12)の平均値から求めた分散分析表を表14に、図2のような市街地の写真による結果(サンプル数:10)の平均値から求めた分散分析表を表15に示します。
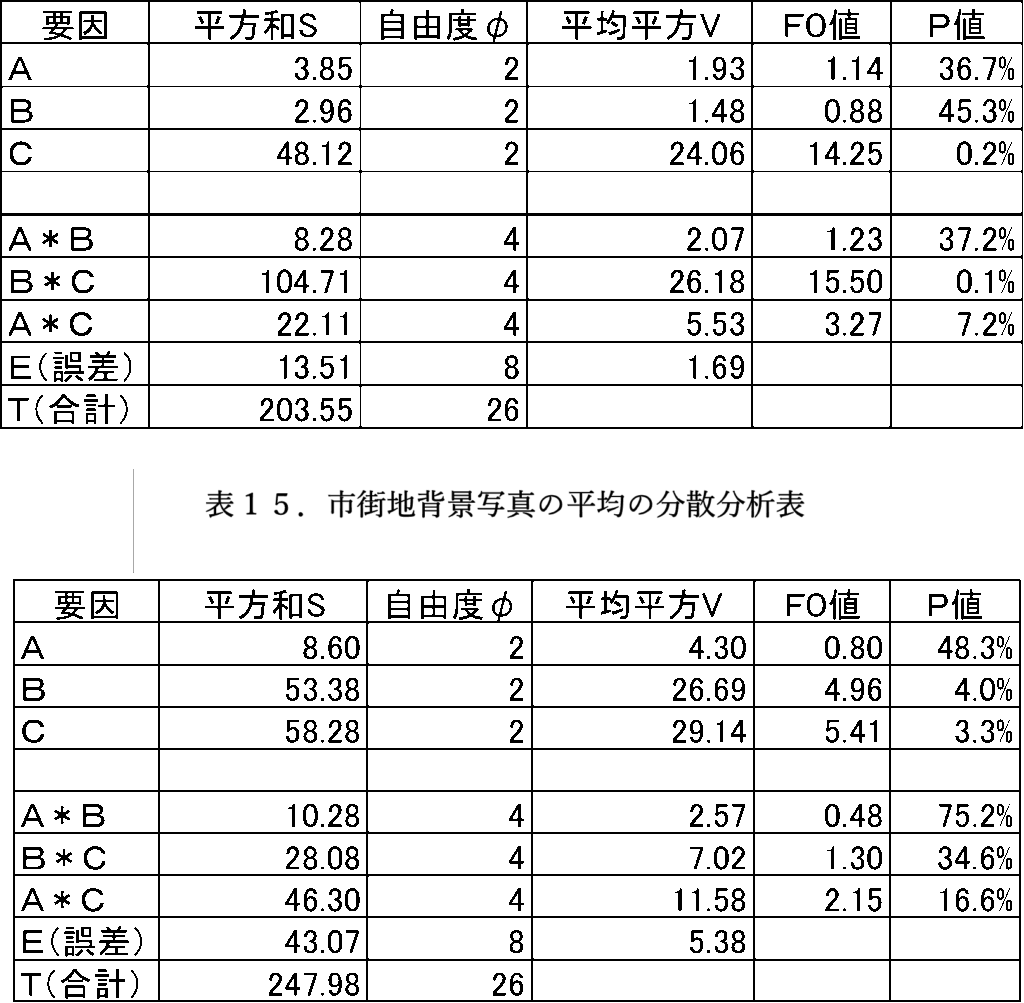
表14より、背景なし写真では、因子Cと交互作用B*Cが高度に有意となりました。表15より市街地の背景写真では、因子Bと因子Cが有意となりました。交互作用は有意とはなりませんでした。このことより、背景なし写真の方の評価が鋭くなると考えられます。また、市街地の写真で因子Bが有意となったことから、背景の影響もあると考えられます。最適水準は、いずれもA2(赤色リボン)、B3(赤色ブレザー)、C3(赤色スカート)となりました。
【5 考察】
以上の結果から、AKB48の前田敦子さんが本校の制服を着た場合、スカートの選択が最も重要であり、スカートとブレザーの組合せにも注意が必要であることがわかりました。男子と女子の感性の違いについては、女子は、スカートとリボンについてもこだわりがあることがわかりました。最適な組合せは、赤色リボン、赤色ブレザー、赤色スカートとなりました。この最適な組合せは、個人の好みにより違うことも分かりました。
アンケートの方法としては、手間暇はかかりますが、個別方式で行う方が特徴がよく出ることが分かりました。
また、今回のような制服の場合には、制服単体だけでなく、背景などの状況も考慮する必要があることがわかりました。
【まとめと今後の課題】
今回、どの組合せの制服が魅力的かについて心理学実験と統計分析を使って研究しました。まず、種々の組合せの合成写真を作成しました。アンケートの方法による影響も評価するため、写真を見せて採点してもらう個別形式と、プロジェクターで投影して採点してもらう集合形式で行いました。統計分析は実験計画法を使い、因子の相互作用についても評価を行いました。その結果、スカートをメインに選び、スカートとの組合せでブレザーやリボンを選んで行けばよいことが分かりました。また、状況に応じて、最適な制服の組合せが異なることや、個人の好みも影響すると思われます。この点については、さらに事例を増やして研究する必要があると考えます。
この心理学実験と統計分析を使えば、新しい製品を開発する際に、製品にどのような機能やデザインを加えたらよいかを定量的に評価できると思います。今後は、色々な分野にこの手法を使ってよりよい製品を開発していきたいと思います。
【7.謝辞】
本研究の心理学実験におけるアンケート方法について、心理学がご専門の先生にご指導いただきましたことに深く感謝致します。
本研究のアンケートに快くご協力頂いた本校の先生並びに、生徒のみなさんに感謝致します。
【本探究活動のまとめ】
今回は、「どの組合せの制服が魅力的か ―心理学実験による統計分析―」の探究活動を紹介しました。
この探究活動の目的は、一つには、生徒が探究学習に興味を持って欲しかったことです。そこで、制服を選ぶという身近な問題をテーマにしました。二つ目は、当時、パソコン同好会では、ワードやエクセル、パワーポイントの検定取得を目標に活動していましたので、エクセルの応用を学んで欲しいと思いました。
はっきり言えば、高校1年生の生徒にとって、実験計画法という統計手法は、理解できなかったと思いますが、写真を見て点数を付けたり、エクセルで計算したりすることはできました。また、何となく実験計画法の雰囲気を掴んでくれたと思います。
この実験計画法を使った探究学習ですが、数年後、工業高校でもテーマを変えて実施しました。これについては、次回(第22回)のブログ記事で紹介します。
冒頭で述べたように、この探究活動の成果をある大学が主催する高校生対象のサイエンスコンテトで発表しました。これに対して、丁寧なコメントを頂きましたので、以下に紹介します。
本研究は、女子の制服であるブレザー、スカート、リボンの魅力的な組み合わせを、実験計画法を使って数値で評価することを試みたものである。
論文は要領よくコンパクトにまとめられていたが、グラフは表計算ソフトの結果をそのまま貼り付けただけのようであった。通常の科学技術論文に掲載されているグラフの書式を参考にされたい。ステージ発表では、図表の数値等が小さかったため後方の聴衆には判読が難しかったのではないかと思われる。さらに、支持棒またはマウスカーソル等を使って図表を示して説明していなかったため、短い時間で図表の意味を理解することは困難であった。パネル展示発表では、実験計画法の計算方法だけではなく、何故そうしたのかという理由を確率・統計の理論に基づいて説明して欲しかった。
ものづくりには、広義の意味のデザイン(設計)という行為が重要で、その中には教義の意味のデザイン(意匠)、機能、性能等の検討や計画も含まれている。本研究は、狭義の意味のデザインを定量的に評価するだけで終わっていたが、ものづくり部門の研究として、その評価がどのようにものづくり、ここでは制服づくりに活かされるのかを考察して欲しかった。
人間のあいまいな感性を定量的に評価することは感性評価と呼ばれているが、今後のものづくりにとってますます重要になるのではないかと思われる。これからも確率・統計の習得に研鑽し、感性評価の研究に取り組まれることを期待する。
高校生には、高すぎるレベルではありますが、目指すべき方向を示して頂き感謝しております。指導教員の私に対するコメントと認識しています。ただ、研究内容に関する指摘が全くありません。実験計画法に関して、知らないのか、興味が無いのでしょうか。
ここまで読んでくれて、ありがとうございます。
ご質問・ご意見・ご感想等がありましたらコメントください。
テラオカ電子
【イチオシのYouTube動画】
このコーナでは、記事に関連する(関連しないかもしれません)気になるYouTube動画を紹介しています。今回は、サトマイさんの『【勉強法】要領のいい学び方』(2024)を紹介します。この動画の冒頭で、今年(2024年)のトレンドの一つとして「努力ブームの到来」が語られています。そういえば、『独学○○』とかいう書籍がよく売られているようです。これがブームになるのかどうかは、分かりませんが、私は、これまで景気が悪くて努力の成果がなかなか出にくい時代だったが、株価の高騰を反映して景気が良くなりそうなので、これから努力が報われやすくなるからだと解釈しています。皆さんはどうお考えでしょうか。一方で、脳科学者の中野信子さんは、努力の才能は遺伝で決まっていますと身も蓋もない話をされていますが、ここでは、努力に向く人とそうでない人がいるので、それぞれのタイプにあった「努力」が重要と説明されています。第15回のブログ記事で、「自分が価値を置くものに向かってこつこつ努力する姿ほど素晴らしいものはない」という価値観を紹介しましたが、結局、「努力」が苦手でもなんでも、「努力」するしかないというブームが来たということでしょか。最後に、どこまでも「努力」が必要だという歌として、Mr.Children の『終わりなき旅』(1998)で締めたいと思います。
「サトマイ:【勉強法】要領のいい学び方 #努力ブーム」
「中野信子『努力ができる才能は、遺伝により決まっている』」
「Mr.Children 「終わりなき旅」 MUSIC VIDEO」
【2024/02/12投稿】

















