「CNN(畳み込みニューラルネットワーク)による画像分類の研究 -CNNの構造の違いによる学習の進み方の比較-」の探究活動
皆さん、こんにちは。テラオカ電子です。今回は、AIの工程(作り方)を学ぶことを目的とした探究活動を紹介します。
私は、これから高校生がAIを学んでいく際、3つの軸で取り組むのが良いと考えています。一つは、「AIの仕組み」、二つ目は、「AIの活用」、そして三つ目が「AIの工程(作り方)」です。
「AIの仕組み」を学ぶ探究活動は、第9回のブログ記事で紹介した「AIとジャンケン」や第27回の「ニューラルネットワークの見える化」があります。
また、「AIの活用」を学ぶ探究活動は、第3、4回の「いじめの研究」や第8回の「高齢者施設訪問」、第16回の「漫才の面白さの研究」で紹介しています。
今回紹介する「AIの工程(作り方)」を学ぶ探究活動には、第6回の「AIとハト」、第14回の「ダイスmusic」があります。
探究活動を、はっきりと3つに区分できるものではありませんが、私は、教材を作る際、どこに重点を置くかを意識して作っています。今回は、「AIの工程(作り方)」の中で、特にCNN(畳み込みニューラルネットワーク)の構造を理解することをコンセプトにしました。
この探究活動は、サイエンスコンテストで発表しなかったのですが、県の産業教育の「生徒研究文」に投稿しました。結果、幸いなことに賞を頂きました。このことで、学校の新聞(卒業式や終業式で配布されます)で生徒が感想を述べていますので紹介します。
課題研究『CNNによる画像分類の研究』を終えて
3年5組 N.K(生徒)
みなさんはGoogleの画像検索を使ったことがありますか?検索にかけた画像の特徴を読み取って、インターネットの中から似た画像を出してくれる機能です。一般的に、画像のAI技術には、ディープラーニングの一つであるCNN(畳み込みニューラルネットワーク)が使われています。
私たち「テラゼミ班」は、このCNNの構造の違いによる「学習」の進み方を研究しました。私がこの研究テーマを選んだ理由は、以前から画像分類の技術を学びたいと思っていたところ、寺岡先生が課題研究のテーマとしてこのAI技術を提示してくれたからです。
CNNの良さは、その分類させる画像の複雑さに影響を受けるため、どの様なCNNの構造が良いかは試行錯誤が必要になります。そこで研究では、5種類の構造のCNNを用意し、各CNNの構造が学習に及ぼす影響を調べました。具体的には、ニッパー、ワイヤストリッパーおよびドライバーの3種類の工具を各30枚撮影し、ラズベリーパイを使って用意したモデルを学習させました。そして、5つのモデルの正解率と損失誤差を比較・分析しました。
この課題研究では、AI技術の「データ準備」→「モデル定義」→「学習」→「評価」という一連の「AIの工程」を体験しました。AIの研究というと華やかな計算というイメージがありますが、実際は地道な試行錯誤が必要でした。また、研究方法についても学びました。研究とは、「①問い立て、②仮説を作り、③検証を行ない、④結果を発表する」ことと教えられました。「④結果の発表」では大学主催のサイエンスコンテストで、論文投稿とプレゼンテーション発表を行いました。私は、進学する入学試験で面接とプレゼンテーションがあったのですが、このテラゼミで学んだ研究方法の知識を活かすことが出来ました。
[サイエンスコンテストで発表したとありますが、このテーマでは発表していなくて、彼はグループの一員として別のテーマで発表しました]
私が最近観た映画に『ダイ・ハード4』があります。そこでは主人公がピンチの時「確かに俺はコンピュータに弱いさ。それでも生きてるぜ。」と言うセリフがあります。コンピュータやAI技術の進歩は速くて追いつくのが大変ですが、進学先ではこの課題研究で得た力を武器に生きていこうと思います。
では、いつものように、N.K君らが学科の「課題研究成果発表会」で発表した内容を私が代読した形ですが、YouTubeで一般公開しました。以下のリンクから動画を視聴できます。見て頂けると後の話が良く分かると思います。
【CNN(畳み込みニューラルネットワーク)による画像分類の研究」(2021)を公開します。】はこちらから】
それでは、生徒たちの探究活動を紹介します。
【タイトル】CNN(畳み込みニューラルネットワーク)による画像分類の研究-CNNの構造の違いによる学習の進み方の比較-
【1目的】
機械学習において、画像分類には、一般的にCNN(畳み込みニューラルネットワーク)が使われている。しかし、どのような構造のCNNが良いかは、その分類させる画像の複雑さに影響を受けるため、簡単にはわからない。そのため試行錯誤が必要とされる。
そこで、筆者らは、書籍を参考に5種類の構造のCNNを準備し、実際にオリジナルの画像を学習させて、そこでの学習の進み方を分析することにした。
本研究は、CNNの構造の違いによる学習の進み方を分析することで、CNNの構造の学習に及ぼす影響を調べることを目的とする。
【2研究方法】
一般的に、ディープラーニングの開発は、図1に示すようなプロセスで行うとされている。以下にこのプロセス順に研究方法を述べる。
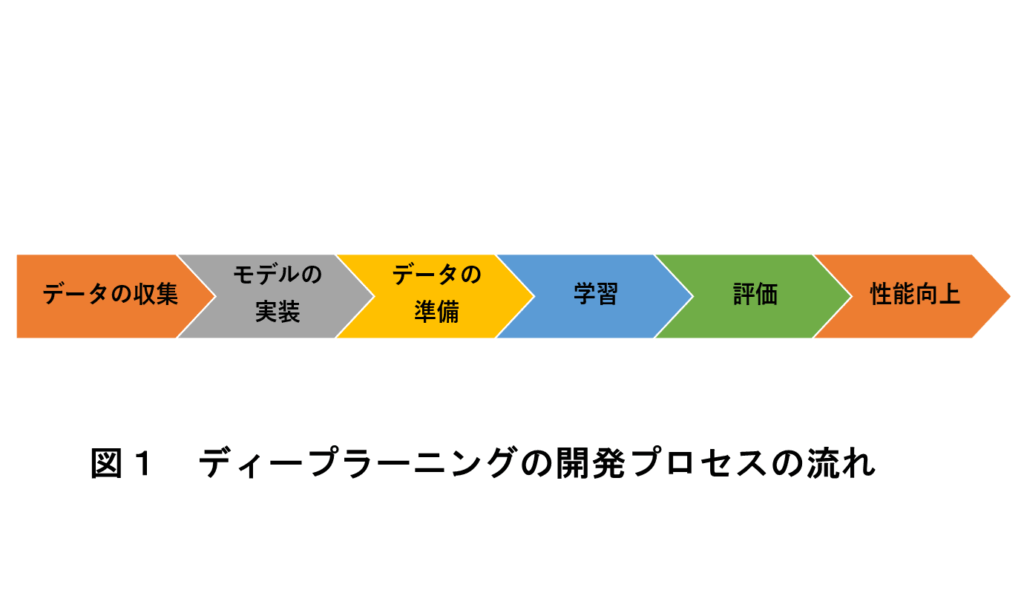
2.1データの収集
本研究では、3種類の工具(ニッパー(Cutting nippers)、ワイヤーストリッパー(Wire stripper)およびドライバー(Driver))の分類を行う。汎用的な分類を行うためには、いろいろなタイプのワイヤーストリッパー等を準備する必要があるが、今回は、研究目的から、各工具を1個準備し、それらを学習、分類することにした。
2.2モデルの実装
課題に合うディープラーニング技術の種類(タスク)を決め、その中でベースとなるモデルを選定する。
本研究では、VGG likeと呼ばれるモデルを基本に実装する。VGGは2014年のILSVRCで、ローカリゼーション(画像のどこに何があるのかを検出する)分野で1位、画像分類分野にて2位に輝いたアルゴリズムである。VGG likeは、これに似せたモデルである。このモデルを基準に、より単純化したモデルを4つ設定する。これらモデルは全てCNNを使っている。CNNの詳細については、後述する。
2.3データの準備
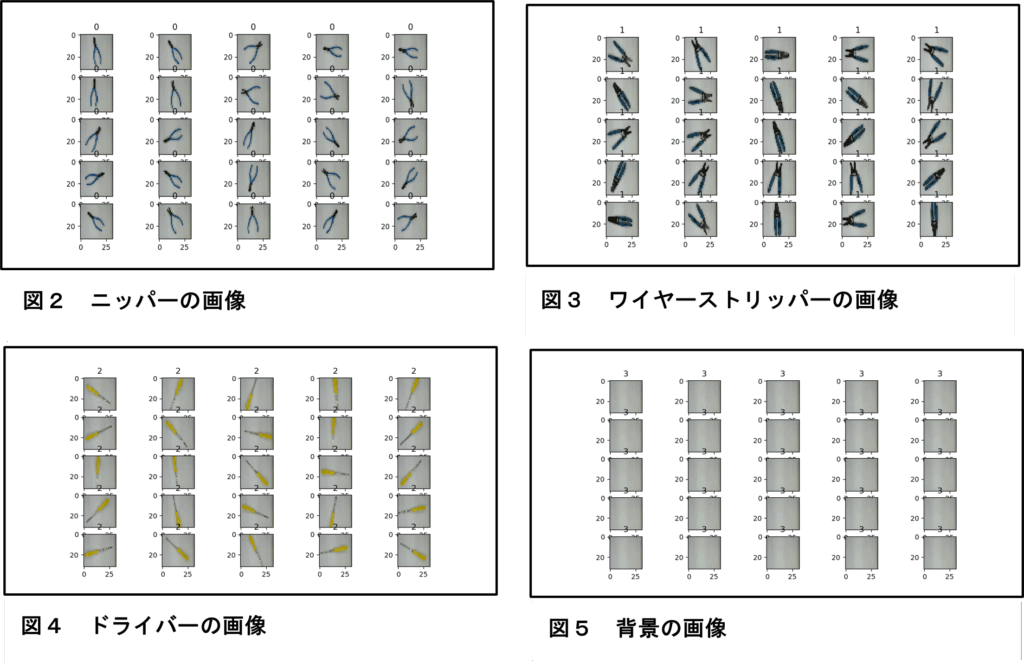
学習に必要なデータと評価に必要なデータを準備する。ラズペリーパイにUSBカメラを付け、実習室にあった3種類の工具と背景の画像を撮影した。それぞれの工具の位置と向きを変えて各30枚撮影した(合計120枚)。そして撮影した写真の画像サイズを32×32ピクセルに変換した。図2(ニッパー)、図3(ワイヤーストリッパー)、図4(ドライバー)および図5(背景)に、変換後の画像を示す(最初の25枚を表示している)。画像サイズを32×32ピクセルに変換したのは、CIFAR-10のデータセットが32×32ピクセルであることから、本研究の画像もその複雑さから同様に扱ってよいと考えたからである。なお、CIFAR-10とは、6万枚の物体カラー写真(乗り物や動物など)の「画像+ラベル」データが無料でダウンロードでき、画像認識などのディープラーニングの評価によく利用されているものである。
2.4 学習
準備したデータを基にモデルの学習を行う。実装しただけの何も学んでいないモデルは、ランダムな答えを返す。そのランダムな答えを、用意したデータを基に訂正する「学習」のサイクルを回すことで、モデルは有益な回答を出力する。
本研究では、5つのモデルを準備してその「学習」の違いを正解率(Accuracy)と損失誤差(loss)を使って評価する。
本研究では、フレームワークとしてTensorFlow、Kerasを使った。それぞれのバージョンは、
TensorFlow == 1.14.0
Keras == 2.2.4
である。ちなみに、ラズベリーパイは、バージョンの違いで、うまく動かないことがある。
学習で使ったオプティマイザーは、rmsprop、損失関数は、交差エントロピー誤差(categorical _crossentropy)、metricsは、accuracyである。
学習データは、3つの工具と背景の画像が各30枚の合計120枚である。そこから7割の84枚を学習用、残りの36枚を検証用画像とし、さらに過学習を防ぐために学習用の画像をデータ拡張した。データ拡張は、プラスマイナス30度から2度ずつ傾けた画像に拡張した。そうすることで、学習用画像は、2520枚になった。さらに、ドロップアウトも使用した。ドロップアウトの畳み込みブロックでの使用割合は、0.25、全結合層では、0.5とした。
学習のバッチサイズは、256、エポック数(学習更新回数)は、21回である。バッチサイズは大きい方が望ましいが、ラズベリーパイのメモリの制限からこの値とした。
本研究では、モデルの違いを確認するため、上記の条件(学習データ、ドロップアウト率、バッチサイズおよびエポック数)は全て同じとした。
2.5 評価
学習したモデルが目的に見合っているかを確認する。どれだけ正しい出力を行っているかを検証する。
本研究では、学習の進行状況を学習データと検証データそれぞれについて、正解率(Accuracy)と損失誤差(loss)をグラフに表示して確認する。
2.6 性能向上
評価した結果を基にモデルの修正やデータの整理/加工、学習時のパラメータ調整を行い、再度学習と評価のサイクルを繰り返す。
本研究では、工具の分類という汎用性能の向上を目的としないため、5つのモデルの違いによる学習の進行状況の考察に留める。
2.7 CNN(畳み込みニューラルネットワーク)とは
畳み込みニューラルネットワーク(Convolutional Neural Network: CNNまたはConvNet)とは、何段もの深い層を持つニューラルネットワークで、特に画像認識の分野で優れた性能を発揮しているネットワークである。このネットワークは「畳み込み層」や「プーリング層」などの幾つかの特徴的な機能を持った層を積み上げることで構成され、現在幅広い分野で活用されている。
本研究では、画像分類を扱うので、このCNNのモデルで評価を行った。
【3実験結果】
3.1 モデルの構造と学習時間
準備したCNNの構造は、以下の5つである。
- VGG like(モデルA)
基本としたモデルである。1エポックの学習時間は、約30秒であった。
以下に、モデルの構造を示す。なお、ここでのモデルの表示は、Kerasの model.summary() 関数を使った出力である。
Model: “sequential”
_________________________________________________________________
Layer (type) Output Shape Param #
=========================================
conv2d (Conv2D) (None, 30, 30, 32) 896
_________________________________________________________________
conv2d_1(Conv2D) (None,28, 28, 32) 9248
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None,14,14,32) 0
_________________________________________________________________
dropout (Dropout) (None, 14, 14, 32) 0
_________________________________________________________________
conv2d_2 (Conv2D) (None, 12, 12, 64) 18496
_________________________________________________________________
conv2d_3 (Conv2D) (None, 10, 10, 64) 36928
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None,5,5, 64) 0
_________________________________________________________________
dropout_1 (Dropout) (None, 5, 5, 64) 0
_________________________________________________________________
flatten (Flatten) (None, 1600) 0
_________________________________________________________________
dense (Dense) (None, 512) 819712
_________________________________________________________________
dropout_2 (Dropout) (None, 512) 0
_________________________________________________________________
dense_1 (Dense) (None, 4) 2052
==========================================
Total params: 887,332
Trainable params: 887,332
Non-trainable params: 0
- 畳み込みブロックの畳み込み層を1層にしたモデル(モデルB)
VGG like(モデルA)は、畳み込みブロックにおいて畳み込み層を2層で構成しているが、ここでは1層に単純化した。1エポックの学習時間は、約12秒であった。
Model: “sequential”
_________________________________________________________________
Layer (type) Output Shape Param #
==============================================
conv2d (Conv2D) (None, 30, 30, 32) 896
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None,15,15,32) 0
_________________________________________________________________
dropout (Dropout) (None, 15, 15, 32) 0
_________________________________________________________________
conv2d_1 (Conv2D) (None, 13, 13, 64) 18496
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None,6,6, 64) 0
_________________________________________________________________
dropout_1 (Dropout) (None, 6, 6, 64) 0
_________________________________________________________________
flatten (Flatten) (None, 2304) 0
_________________________________________________________________
dense (Dense) (None, 512) 1180160
_________________________________________________________________
dropout_2 (Dropout) (None, 512) 0
_________________________________________________________________
dense_1 (Dense) (None, 4) 2052
=========================================
Total params: 1,201,604
Trainable params: 1,201,604
Non-trainable params: 0
- 畳み込みブロックを1層、全結合層のユニットを半減にしたモデル(モデルC)
②から畳み込みブロックを1層にし、さらに全結合層のユニット数を512から256に半減した。1エポックの学習時間は、約7秒であった。
以下に、モデルの構造を示す。
Model: “sequential”
_________________________________________________________________
Layer (type) Output Shape Param #
=========================================
conv2d (Conv2D) (None, 30, 30, 32) 896
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None,15,15,32) 0
_________________________________________________________________
dropout (Dropout) (None, 15, 15, 32) 0
_________________________________________________________________
flatten (Flatten) (None, 7200) 0
_________________________________________________________________
dense (Dense) (None, 256) 1843456
_________________________________________________________________
dropout_1 (Dropout) (None, 256) 0
_________________________________________________________________
dense_1 (Dense) (None, 4) 1028
=========================================
Total params: 1,845,380
Trainable params: 1,845,380
Non-trainable params: 0
- 畳み込み層のカーネル数、全結合層のユニット数を半減したモデル(モデルD)
モデルCから畳み込み層のカーネル数を32から16に半減、さらに全結合層のユニット数を256から128に半減した。1エポックの学習時間は、約4秒であった。
以下に、モデルの構造を示す。
Model: “sequential”
_________________________________________________________________
Layer (type) Output Shape Param #
===============================================
conv2d (Conv2D) (None, 30, 30, 16) 448
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None,15,15,16) 0
_________________________________________________________________
dropout (Dropout) (None, 15, 15, 16) 0
_________________________________________________________________
flatten (Flatten) (None, 3600) 0
_________________________________________________________________
dense (Dense) (None, 128) 460928
_________________________________________________________________
dropout_1 (Dropout) (None, 128) 0
_________________________________________________________________
dense_1 (Dense) (None, 4) 516
=========================================
Total params: 461,892
Trainable params: 461,892
Non-trainable params: 0
モデルDから畳み込み層のカーネル数を、さらに16から10に減少、加えて全結合層を1層に削減した。1エポックの学習時間は、約3秒であった。
以下に、モデルの構造を示す。
Model: “sequential”
_________________________________________________________________
Layer (type) Output Shape Param #
=========================================
conv2d (Conv2D) (None, 30, 30, 10) 280
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None,15,15,10) 0
_________________________________________________________________
dropout (Dropout) (None, 15, 15, 10) 0
_________________________________________________________________
flatten (Flatten) (None, 2250) 0
_________________________________________________________________
dense (Dense) (None, 64) 144064
_________________________________________________________________
dropout_1 (Dropout) (None, 64) 0
_________________________________________________________________
dense_1 (Dense) (None, 4) 260
=========================================
Total params: 144,604
Trainable params: 144,604
Non-trainable params: 0
モデルの複雑さは、A、B、C、D、Eの順に単純になり、学習時間も順に減少した。ただし、パラメータの総数は、このモデルの複雑さとは関連せず、C、B、A、D、Eの順に減少した。これは、畳込み層は、次元を縮小するので、畳み込み層の数が少ないとパラメータが増えるからである。
3.2 学習時の正解率(Accuracy)と損失誤差(loss)変化
5つのモデルにおける正解率(Accuracy)と損失誤差(loss)変化を以下に示す。
① VGG like(モデルA)
図6に、モデルAの正解率(Accuracy)、図7に、その損失誤差(loss)変化を示す。
訓練データの学習において、精度と損失に大きな振動の推移が見られた。ただし、訓練データと検証データの推移に乖離はみられないので過学習は生じていない。
②畳み込みブロックの畳み込み層を1層にしたモデル(モデルB)
図8に、モデルBの正解率(Accuracy)、図9に、その損失誤差(loss)変化を示す。
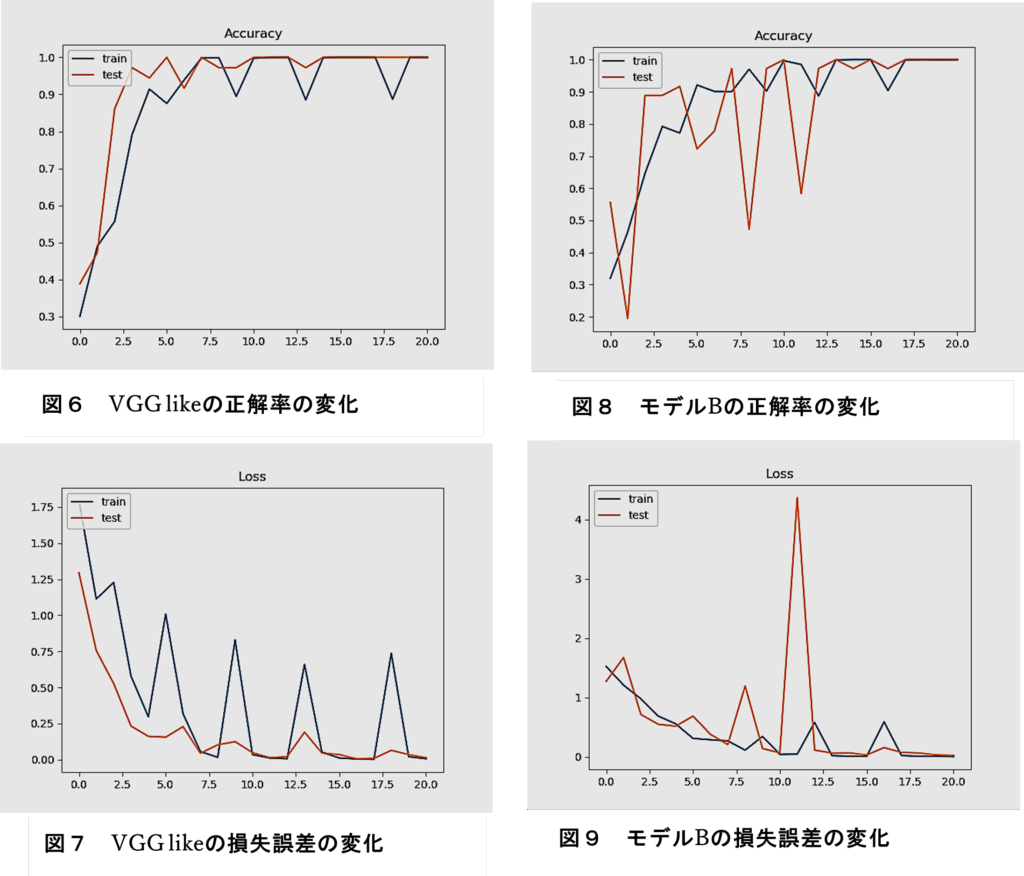
訓練データの学習において、精度と損失に若干振動の推移が見られた。ただし、訓練データと検証データの推移に乖離はみられないので過学習は生じていない。
③畳み込みブロックを1層、全結合層のユニットを半減したモデル(モデルC)
図10に、モデルCの正解率(Accuracy)、図11に、その損失誤差(loss)変化を示す。
訓練データの学習において、精度と損失に僅かに振動の推移が見られた。ただし、訓練データと検証データの推移に乖離はみられないので過学習は生じていない。
④畳み込み層のカーネル数、全結合層のユニット数を半減したモデル(モデルD)
図12に、モデルDの正解率(Accuracy)、図13に、その損失誤差(loss)変化を示す。
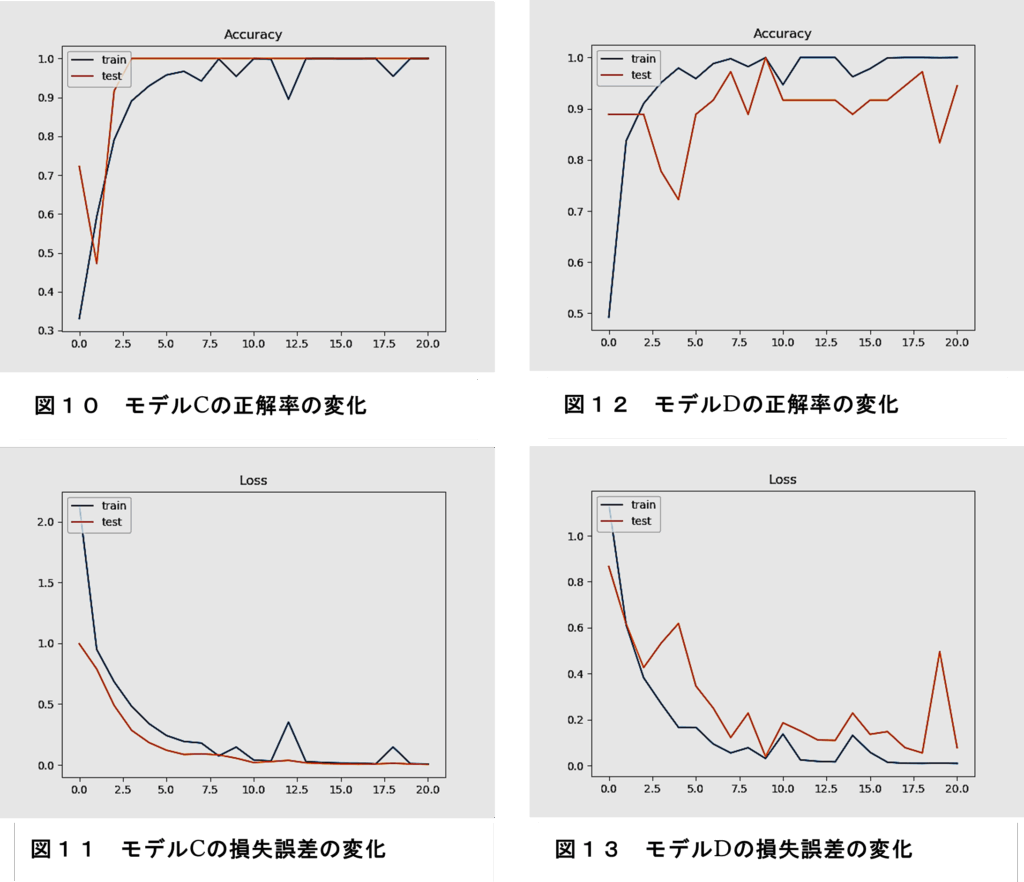
訓練データの学習において、精度と損失に僅かに振動の推移が見られた。また、訓練データと検証データの推移に乖離が見られるので過学習が生じている。
- 畳み込み層のカーネル数低減、全結合層のユニット数を半減したモデル(モデルE)
図14に、モデルEの正解率(Accuracy)、図15に、その損失誤差(loss)変化を示す。
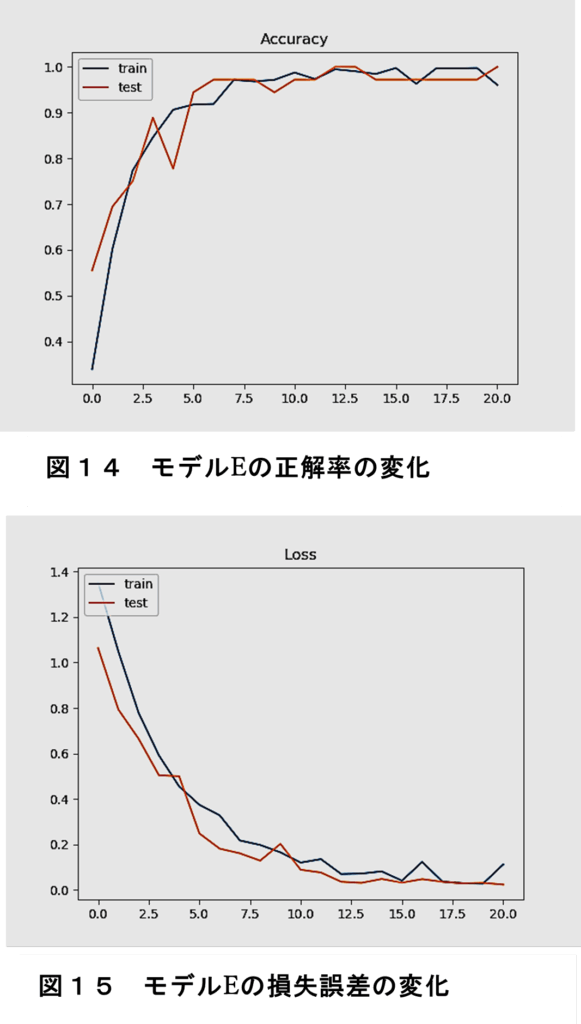
訓練データの学習において、精度と損失に振動の推移は見られなかった。訓練データと検証データの推移にも乖離はみられないので過学習は生じていない。
いずれのモデルでも学習は進み、正解率は、学習データ、検証データとも95%以上になった。損失誤差も、学習が進むにつれ減少している。だたし、損失誤差において、モデルが複雑なほど、その変化が振動する傾向が見られた。
【4考察】
今回の5つのモデルでは、正解率と損失誤差における学習データと検証データに明らかな乖離は見られなかった。このことから過学習は起こっていないと思われる。ただし、モデルDでは、少し乖離があるので、若干の過学習の傾向があったと推察できる。
一般にモデルを複雑にすると、細かな分類ができるようになるが、過学習を起こしやすくなるといわれる。今回、データ拡張を行い、学習データを増やしたことと、ドロップアウトをかなり割合で使用したので、過学習が防げたと考えられる。
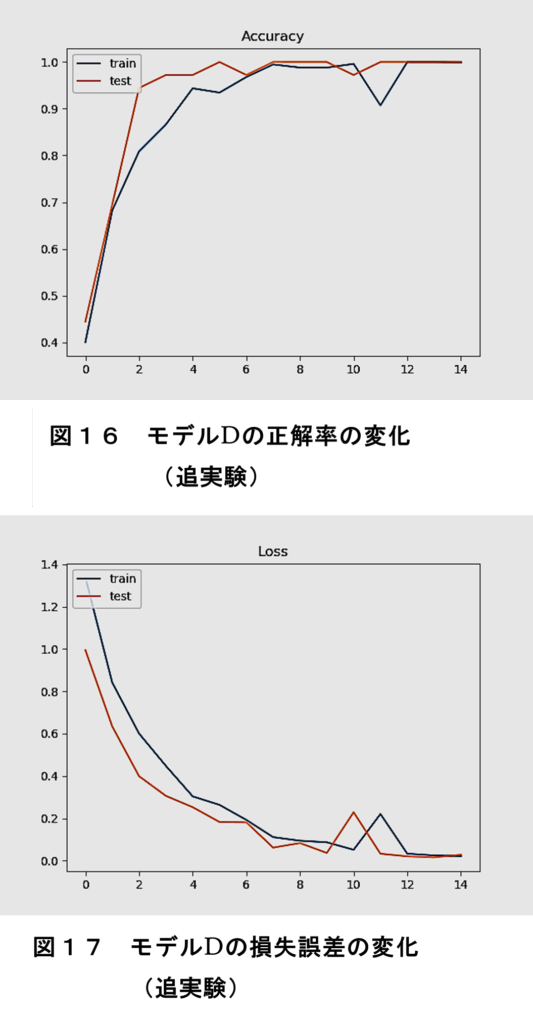
モデルDで過学習の傾向が見られる点について、同じ条件で、再度学習を行った結果を図16、図17に示す。
これらの結果からは、正解率と損失誤差において、学習データと検証データで乖離が見られないので、過学習は生じていないと考えられる。従って、先のモデルDでの過学習の傾向は、パラメータの初期値の影響を受けたものといえる。従って、学習は、複数回行って評価する必要がある。
また、損失誤差において、モデルが複雑なほど、その変化が振動する傾向が見られた。モデルが単純な方が、安定して学習が進むことが分かった。
【5まとめと今後の課題】
本研究は、5つのCNNモデルを準備し、その構造の複雑さによる学習の進み方を分析した。その結果、32×32ピクセルという画素数が少ない画像分類においては、かなり単純なモデルでも学習が進むことが明らかになった。
また、学習データと検証データの正解率と損失誤差の変化から、単純なモデルの方が、正解率と損失誤差が振動しないことや、パラメータの初期値の影響を受けにくい、堅牢なモデルであることを示すことができた。
従って、ディープラーニングの構築は、学習画像の複雑さを考慮し、どこまで単純なモデルで構築するかが要と言える。
今回は、学習データ数やドロップアウトの割合などを一定としたが、今後は、これらの違いによる学習の影響を検証していく。
参考・引用文献
[1] 佐藤諒芽、金沢蓮太郎:『AIとじゃんけん ― 機械学習の「学習」におけるパラメータの可視化による考察―』(2020) 県工業高等学校 生徒研究文
[2] Francois Chollet著、巣籠悠輔監訳:『PythonとKerasによるディープラーニング』(2018)、マイナビ出版
[3] 井上大樹、佐藤俊:『ディープラーニング開発実践ハンズオン』(2021)、技術評論社
[4] クジラ飛行机、杉山陽一、遠藤俊介:『PythonによるAI・機械学習・深層学習アプリのつくり方』(2020)、ソシム
[5] MathWorks,“畳み込みニューラルネットワーク (CNN)”,
https://jp.mathworks.com/discovery/convolutional-neural-network.html (2021年7月8日最終閲覧)
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
【本探究活動のまとめ】
この探究活動では、CNNの構造を変えて、「学習」様子の違いを確かめました。この5つの違いから何か新しい知見が得られたわけではないので、研究としての「深み」はありません。
ですが、違いが起こることが分かっただけでも良かったのではないかと考えています。書籍やネットの情報をそのまま実行して満足していてはいけません。紹介されている方法が最適であるとは限りませんので、自分たちの状況に応じて変えていく必要があります。
また、本「課題研究」は、「AIの工程(作り方)」を学ぶ探究活動なのですが、もちろんこの体験だけで、AIが作れるようになるわけではありません。AIには、様々なタイプがありますので、そのやり方も様々です。ですが、一つの事例を体験することで、AIの具体的なイメージを一つ持つことができたのではないかと思います。生徒たちは、これからも、様々な経験をしていきますが、そもそも「種」がないと、これからの経験が活かせないと考えます。
ところで、冒頭で紹介した感想文の生徒は、公立の短期大学に進学しました。その方に、入試でプレゼン発表があるので指導して欲しいと頼まれました。彼は「課題研究」のメンバーでもあったので、特別に引き受けることにしました。詳しいことは忘れてしまいましたが、テーマは社会問題について自分の意見を述べるもので、形式は、面接時に時間が与えられて、資料なしで口頭説明するようなものだったと思います。
テーマを何にするかを聞いたところ、海洋プラスチック問題にしたいとのことでした。色々話していきながら、彼にしたアドバイスは、マスメディアやネットで言っていることをそのまま言うのではなく、間違っていてもよいので、自分の頭で考えたことをプレゼンした方がよいと伝えました。なぜなら、大学というところは、従来の知識を疑い探究していくところだからです。
以下に、原稿(最終版ではありません。リハーサルを通して変更していきました。でも大筋はこんな感じだったと記憶しています)を掲載します。総合選抜入試の参考にしてください。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
短期大学 入学試験 プレゼンテーション 原稿
テーマ 海洋性プラスチック問題におけるレジ袋の有効性に関する考察
私は、海洋性プラスチックで問題となっているレジ袋について意見を述べます。
まず初めに、レジ袋と海洋性プラスチック問題は、日本については無関係であること述べます。次に、レジ袋は、その利便性と資源の有効性が高いことを述べます。最後に、レジ袋の回収に関して、提案をします。
まず、レジ袋は、日本に限ると海洋性プラスチック問題には、無関係であると考えます。
そもそも海洋プラスチック問題とは、環境省によると、①海岸での漂着ごみ、②マイクロプラスチックの海洋生物への影響、③そのマイクロプラスチックは地球規模で広がっている、と定義されています。
しかし、私は、レジ袋を使わないようにしてもこのような海洋プラスチック問題は解決しないと考えます。
その根拠は、一つは、レジ袋は日本ではほとんど家庭ごみとして回収されているからです。2つ目は、海洋プラスチックの発生は、1位中国、2位インドネシア、3位フィリピンで、この三国で年間557万トンを占めており日本では、わずか6万トンでその割合は上位三国から発生する海洋プラスチックのわずか1パーセントです。3つ目は、マイクロプラスチックのような、小さな粒子は、体積に対する表面積が大きいので分解が早いと考えられます。
以上の理由から、レジ袋を使わないことと海洋性プラスチック問題とは関係が薄いと考えます。
次に、レジ袋は、その利便性と資源の有効性の観点から活用性が高いことを述べます。
私は、レジ袋を、いろいろ活用しています。部屋のごみの収集や、学校に小物をもっていく際の袋としてなどです。安く、丈夫で、軽く、かさばらないので大変便利に活用しています。特に旅行に行く際には、持ち物の仕分けに大変便利です。
ところが、昨年、2020年7月よりレジ袋が有料化されました。私は、買い物の際、レジ袋が買い物に使った後でも役にたつので、時々は、数円かかりますが購入しています。また、レジ袋は、ほとんどが高密度ポリエチレンという材料から作られていますが、石油資源の有効活用の点からも経済的です。それは、高密度ポリエチレンが石油の精製時における余り物として作られる物だからです。
以上より、レジ袋は、その利便性と資源の有効性の観点から活用性が高いといえます。
最後に、レジ袋の回収に関して、私のアイデアを述べます。現在、法律でレジ袋は有料化されています。それは、いわば、レジ袋は、公共財であるともいえます。そこで、レジ袋に、「市回収」のマークを印刷して、レジ袋を家庭ごみの回収用の袋としても使えるようにしたらよいと考えます。そうすれば、レジ袋の活用性が広がるので、確実に回収されることになると考えます。
まとめます。まず、レジ袋は、海洋性プラスチック問題には、日本に限っては無関係であること述べました。そして次に、レジ袋は、その利便性と資源の有効性の観点から活用性が高いことを述べました。最後に、レジ袋の回収に関して、私の提案を述べました。
レジ袋は、日常生活で役に立ち便利です。そして、レジ袋が実際の海洋プラスチック問題に大きく寄与しているとは考えられません。また、マイクロプラスチックについては、普通のレジ袋であっても分解されるのが早いため、海洋汚染とつながらないと考えられます。
現在、プラスチックの使用率を減らすことが、環境に良いと言われていますが、プラスチックは、もともと微生物の死骸からできています。一方、紙は、生きた木を切って使います。考え方によっては、生きた生物を使うよりも死骸を使った方が、エコロジーと言えます。
以上のこの報告は、今説明した根拠によっています。現在わかっていないことがあるかもしれません。現代科学も必ず正しいといえるというわけではありません。間違っていることもあります。今後も調べていきたいと考えています。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
この方は、卒業した1年後、学校に挨拶にきてくれました。色々新しいことを学んで、「目が覚めた」というようなことを言ってくれました。元気そうでなによりでした。この後、私は転勤しましたので、その後の彼について知る由もないのですが、これからも探究を続けて欲しいと思っています。
ここまで読んでくれて、ありがとうございます。
ご質問・ご意見・ご感想等がありましたらコメントください。
テラオカ電子
【イチオシのYouTube動画】
このコーナでは、記事に関連する(関連しないかもしれません)気になるYouTube動画を紹介しています。今回は、EXILEの『EXIT』(2005)を紹介します。この曲は、天海祐希主演のテレビドラマ「女王の教室」のエンディングテーマでした。私は、このドラマを最初から観ていないのですが、話題になっていたこともあり(今では放映できない内容だと思いますが)、終盤(2回ほどですが)観ました。ぜひ、生徒にも観て欲しいと思い、このドラマの名言集(YouTubeチャンネルで多くアップされています)を「課題研究」で紹介していました。生徒からは、「もっと早く観ておきたかった」などという感想を受けました。なぜ勉強しなければならないかが語られています。ちなみに、ある年、この話を課題研究班の担任の先生(当時私は副担任をやっていました)に話したら、この名言をすらすらと言葉にされたのです。小学校の時よく観ていたと話されました。彼は、有名国立大学出身の先生なのですが、私は、この名言が彼の受験勉強のモチベーションになっていたのではないかと勝手に考えています。
「Exit」
「教育者や親が 絶対に聞くべき【女王の教室 阿津真矢 】心に刺さる名言集【Vol. 1】」
【2024/03/23投稿】

















